重（zhòng）链剖分

杨千睿

先说几句

• 树链剖分（树剖/链剖）有多种形式，如 重链剖分，长链剖分 和用于 Link/cut Tree 的剖分（有时被称作“实链剖分”），大多数情况下（没有特别说明时），“树链剖分”都指“重链剖分”。

• 在本文中，一条「链」是指一条深度单调递增的路径。
  
  如图，红色的路径不是一条链，而绿色的路径是一条链。

看一个问题

给你一颗 $n$ 个点的有根树，每个点有点权，支持以下几个操作：

1. 将一个点的子树内的所有点权 $+W$ ;
2. 查询一个点的子树的点权和。

• $n,m\le10^5$.

dfs 序

对一棵树进行 dfs。每访问到一个新的节点，记录下它的编号，如图所示。

容易发现一个性质：每个点的子树的 dfs 序都是连续的。
（正确性显然，因为在 dfs 时必然先访问这个节点，然后再访问孩子）

有了 dfs 序这个工具的帮助，就可以设计出一个比较优秀的算法了：

• 维护一个数列，数列的第 $i$ 项是 dfs 序为 $i$ 的节点的点权。

• 那么，节点 $u$ 的子树其实就是数列中对应编号为 $dfn_u \sim dfn_u+\mathrm{size}(u)-1$ 的节点。（$dfn_u$ 是 $u$ 点的 dfs 序，$\mathrm{size}(u)$ 是节点 $u$ 的子树大小）

• 建立一颗线段树，对于子树的修改和查询操作，就可以转化为序列上的区间操作，每次操作可以以 $\mathcal{O}(\log n)$ 的复杂度完成。

这个问题的加强版

给你一颗 $n$ 个点的有根树，每个点有点权，支持以下几个操作：

1. 将一个点的子树内的所有点权 $+W$ ;
2. 查询一个点的子树的点权和；
3. 将一条路径上的所有点的点权 $+W$ ;
4. 查询一条路径的点权和。

• $n,m\le10^5$.

问题分析

• 1 和 2 操作可以使用 dfs 序 + 线段树实现，3 和 4 操作可以使用树上倍增、树上差分等技巧实现。

• 但这些方法都不能同时支持 1234 操作。

• 那么就需要重链剖分算法来实现了。

• 事实上，重链剖分和 dfs 序思路类似，也是将树上问题转化为序列问题，使用线段树求解。

大体思路

仍然使用 dfs 序的方法维护操作 12，现在只需要解决操作 34 即可。

可以发现，在进行 dfs 的时候，有一些链上的点的 dfs 序也是连续的（因为 dfs 的时候这些点的访问顺序是连续的），我们暂且称这样的链为「树链」，如图所示：

绿色的链就是树链。而且，我们把单独的一个点也当作一条树链。

核心思路

• 那么，我们就可以快速地查询和修改一条树链上的点权了。但是，如果要操作的路径不是一条树链呢？

• 重链剖分的关键思路：跳链

• 要维护从 $u$ 到 $v$ 的一条路径，设 $u$ 所在的树链的链顶为 $top_u$，$v$ 所在的树链的链顶为 $top_v$，设 $\mathrm{dep}(top_v)<\mathrm{dep}(top_u)$。

• 那么一定有：$u$ 点到 $top_u$ 点的路径一定是 $u$ 点到 $v$ 点的路径的子路径。

举个例子

设 3 号点为 $u$ 点，11 号点为 $v$ 点，$\mathrm{dep}(top_3)<\mathrm{dep}(top_{11})$。

$u$ 点到 $top_u$ 点的路径一定是 $u$ 点到 $v$ 点的路径的子路径。

证明

反证法：假设 $\mathrm{lca}(u,v)$ 在 $u$ 到 $top_u$ 的路径上（此时 $u$ 点到 $top_u$ 点的路径不是 $u$ 点到 $v$ 点的路径的子路径），那么 $\mathrm{dep}(top_v)<\mathrm{dep}(\mathrm{lca}(u,v))<\mathrm{dep}(top_v)$，矛盾。

• 那么我们每次就可以把这样的 $u$ 节点跳到 $fa(top_u)$ 节点上，并且利用线段树，修改或查询 $u$ 到 $top_u$ 这段路径（这段路径的编号一定是连续的）。
• 跳完之后的 $u$ 节点就到了一条新的链上，然后再和另一个节点进行比较，重复这样「跳」的操作。
• 直到 $u$ 和 $v$ 在同一条链上，那么此时再对 $u$ 到 $v$ 的路径进行操作即可。
• 值得一提的是，当 $u$ 和 $v$ 跳到同一条链上时，深度较小的点就是这两个点的 LCA。
• 因为「跳链」操作总是向深度较小的地方跳，且永远不会比 LCA 深度小。所以当最后不能再跳时，就是 LCA。

复杂度分析

• 一条链上的树链个数的数量级是 $n$，所以 34 号操作的复杂度就是 $\mathcal{O}(n\log n)$。

• 好像比暴力还慢……

• 辣鸡算法，白讲了

• 这是因为划分树链还有讲究，一个优秀的树链划分方法（其实就是 dfs 顺序）能将一条路径上的树链个数的数量级控制在 $\log n$.

• 这种树链划分方法称为 重链剖分

一些定义

重儿子：对于非叶节点 $u$，它的重儿子 $v$ 是 $u$ 的所有儿子中子树大小最大的。

重边：对于非叶节点 $u$，设它的重儿子为 $v$，边 $(u,v)$ 称为一条重边。

重链：重边首尾衔接形成的链称为重链。

轻儿子：对于非叶节点 $u$，它的轻儿子是除重儿子之外的其他所有儿子。

轻边：对于非叶节点 $u$，设它的一个轻儿子为 $v$，边 $(u,v)$ 称为一条轻边。

链头：对于一条重链，深度最小的节点称为链头。

举个例子

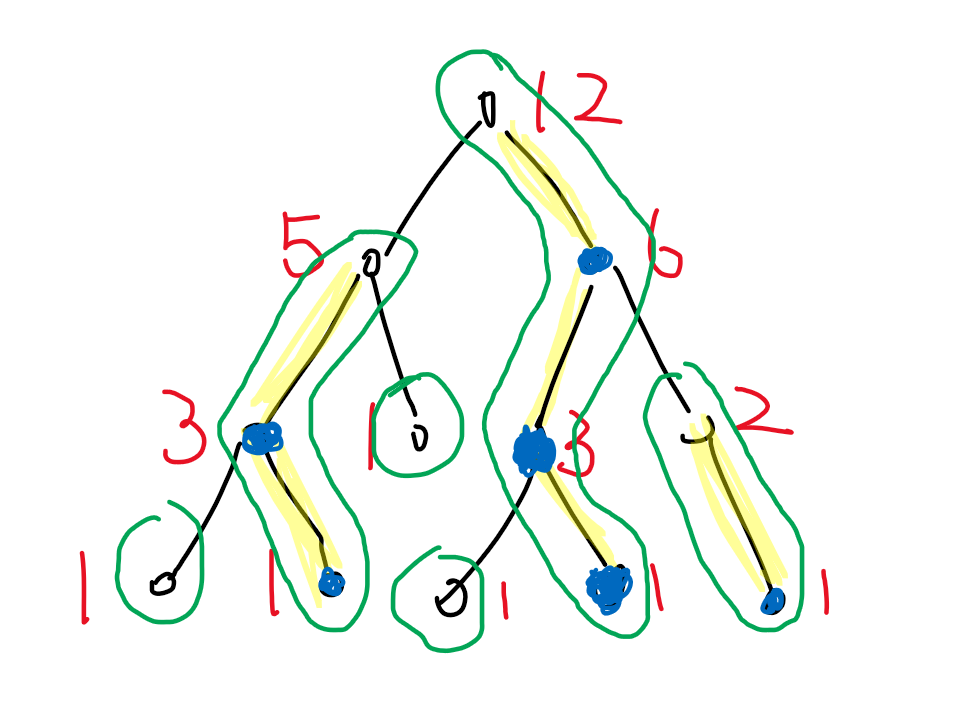
红字是子树大小，蓝点是重儿子，白点是轻儿子，黄色标记出的边是重边，绿色圈圈出的是重链。
注：落单的结点也当作重链。

一条路径上重链的条数的数量级是 $\log n$.

证明：

• 若 $y$ 点是 $x$ 点的轻儿子，即边 $(x,y)$ 是轻边，则 $\mathrm{size}(x) ≥ 2\mathrm{size}(y)$（否则 $y$ 节点就一定是重儿子）。
• 因此从叶子节点走到根节点时，每经过一条轻边，所在的子树的大小就要至少翻两倍。
• 所以一个点到根的路径上，轻边的数量级是 $\log n$。
• 由于重链不相连，两条重链之间至少有一条轻边连接。所以一个点到根的路径上，重链的数量级是 $\log n$.
• 所以任意一条路径上，重链的数量级是 $\log n$.

所以把这颗树的重链作为树链，34 操作的复杂度是 $\mathcal{O}(\log^2 n)$，可以接受。

总结一下

重链剖分要做的事就是通过 轻重边剖分 把树分成许多条链，对每个节点用 dfs 序重新编号，把树上问题转化为序列问题，以套用其他链状数据结构（如线段树等）来维护，这样就可以非常方便的处理同一条链上的若干点/边。

重链剖分可以做的事情有：

• 路径上维护：修改、查询树上两点路径权值和、最值等信息
• 子树维护：修改、查询一颗子树的权值和、最值等信息
• 求最近公共祖先

具体实现

• 如何把重链作为树链呢？
• 回忆一下，树链的定义是编号连续（也就是访问顺序连续）的一条链。
• 那么就要连续的访问重链。对于每个点来说，就是先访问他的重儿子，再访问其他轻儿子。这样，重儿子显然会被连续访问，那树链也就是重链了。

举个例子

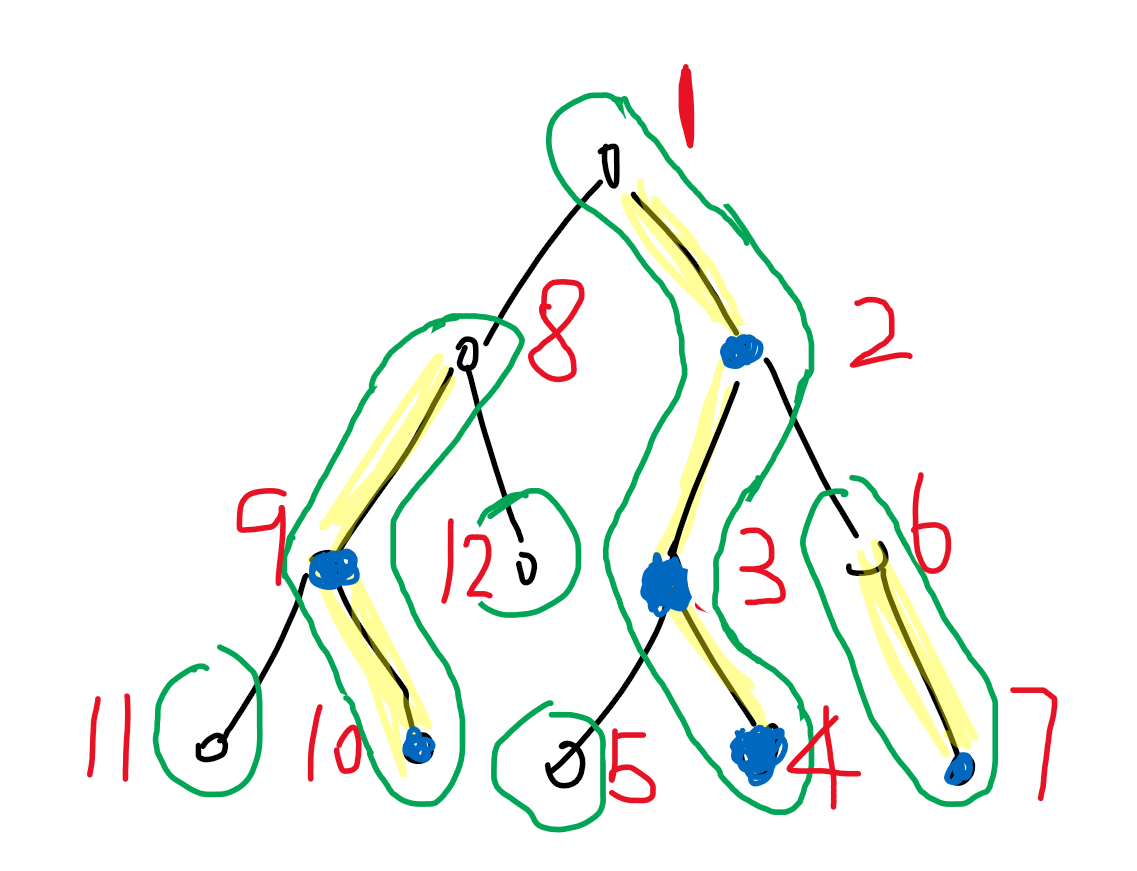
如图所示，红字就是 dfs 序。

使用这种方法，就可以完成 1234 四种操作了。

代码实现

• 两次 dfs 预处理
  • 第一次 dfs 求出每个点的子树大小和重儿子；
  • 第二次 dfs 记录 dfs 序。
• dfs 两次，求出重要的量：
  • $son_x$：$x$ 的重儿子
  • $dfn_x$：$x$ 在 dfs 序中的编号
  • $top_x$：$x$ 所在重链的链顶
  • 若 $(x, y)$ 是重边，则 $top_y = top_x$
    若 $(x, y)$ 是轻边，则 $top_y = y$

代码

（LuoguP3384 【模板】轻重链剖分）

代码

（LuoguP3384 【模板】轻重链剖分）

代码

（LuoguP3384 【模板】轻重链剖分）

代码

（LuoguP3384 【模板】轻重链剖分）

代码

（LuoguP3384 【模板】轻重链剖分）

树链剖分求 LCA

复杂度为 $\mathcal{O}(\log n)$，且常数较小。

例题：P2146 [NOI2015] 软件包管理器

• 裸题

• 每次安装软件，就把根节点到 $x$ 软件路径上的值全部变为 1

• 同理，每次卸载软件，就把 $x$ 以及它的子树的值变为 0

• 线段树维护即可

例题：P3979 遥远的国度

• 路径修改操作不会受到换根影响
• 以一号点为根，进行树链剖分，线段树维护最小值和区间修改
• 记录当前实际的根 root，分类讨论 root 与查询节点 $x$ 的位置关系（以一号点为根）
  1. root 不在 $x$ 的子树内：$x$ 实际子树不变
  2. root 就是 $x$： $x$ 的实际子树是整棵树
  3. root 在 $x$ 的子树里：设 $y$ 是 $x$ 的儿子，且 $y$ 是 root 的祖先，那么 $x$ 的实际子树是 $y$ 的补集。

例题：P1505 [国家集训队] 旅游

• 此题难点在于把边权转换为点权
• 把边 $(u,fa(u))$ 的边权当作 $u$ 点的点权即可
• 那么对一条链 $(u,v)$ 进行操作时需要去除 $\mathrm{lca}(u,v)$ 这个点
• 其他的这些操作都在线段树上很好实现。

题单：

• 【模板】轻重链剖分

• [NOI2015] 软件包管理器

• 遥远的国度

• [国家集训队] 旅游

• 洛谷题单：树链剖分练习题

参考资料：

• 树链剖分 - OI Wiki
• 洛谷日报 树链剖分详解

这次是真的没了